Mioara Joldes

LAAS-CNRS
7 Avenue du Colonel Roche,
31077 Toulouse, Cedex 4 France

phone:(+33) (0)5 61 33 69 26
email: joldes AT laas DOT fr

CV, Publications and Software, Talks, Miscelaneous.

Researcher (DR) at CNRS in the ROC team, at LAAS.

Research Themes and Objectives

bookRigorous computing (validated computing): use numerical computations, but provide mathematical statements about the obtained result, such as sure, yet reasonably tight, error bounds. Build efficient symbolic-numeric objects, algorithms and software tools with direct applications in control of dynamical systems and in particular in the aerospace domain. Use and develop expertise and ideas from Computer Arithmetic and Computer Algebra. See for instance my Habiliation (HDR) defended June 2019 or the HDR Slides.


A. Computer Arithmetic:

Interested in improving the quality (in terms of accuracy, speed, reliability of software, etc.) of the arithmetic available on computers. Check the 2nd edition of Handbook of Floating-Point Arithmetic, Birkhäuser (2018) [B1], coordinated by Jean-Michel Muller. Some results:
With Valentina Popescu and Jean-Michel Muller, we developed algorithms for fast and certified multiple precision arithmetic operations (also tuned for Graphics Processing Units)[J4], [J7], [J8], [C8], [C13]. Related talks: [ASAP14] [Henon13][SMC14][ICMS16]

Efficient and reliable implementation and evaluation of elementary functions: with D. Arzelier and F. Bréhard, we presented at Arith (2019) an exchange algorithm for evaluation and approximation error-optimized polynomials  [C3]. With B. Pasca, we received the Best Paper Award at ASAP 2020, for an efficient FP implementation of the Probit function on FPGAs  [C1].

Error analysis of numerical routines: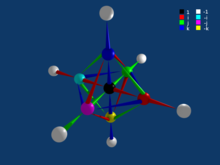

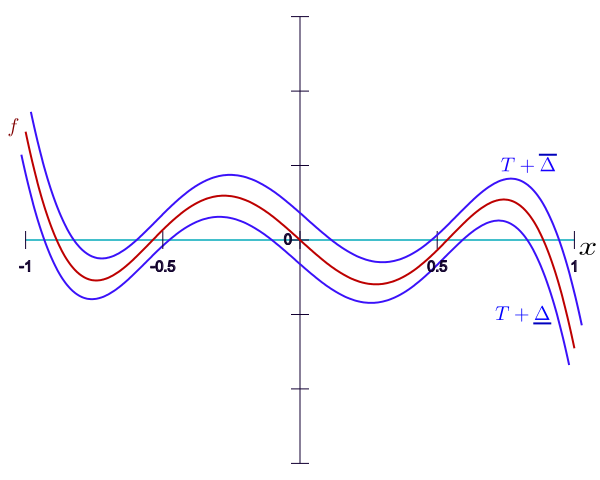
  • quaternions algorithms, with J.-M. Muller, at Arith (2020) [C2];
  • Fast Fourier Transform, with J.-M. Muller, N. Brisebare, J. Picot and A.-M. Nanes, in ACM TOMS (2020)  [J1].

B. Rigorous Polynomial Approximation (RPA): a polynomial approximation together with rigorous error bounds. Use Taylor Models [J9, C22, C23, C17] and Chebyshev polynomial interpolation/series Models [C19], [R3, Chap. 4]. Adapt to rigorous computations many numerical algorithms based on Chebyshev/Taylor Series for solving ordinary differential equations, quadrature, etc. Recent results: compute rigorous uniform approximations based on Chebyshev Series for D-finite functions, i.e. solutions of ordinary differential equations with polynomial coefficients [J5] e.g., erf, exp, sin, Bessel, Airy functions.

With Florent Bréhard and Nicolas Brisebarre, we developed a validated numerics method for the solution of linear ordinary differential equations (LODEs). A theoretical and practical complexity analysis of a so-called a posteriori quasi-Newton validation method is given in [J3].

Objectives: efficient implementation of operations with Chebyshev Models, extensions to multivariate functions; efficient finite precision evaluation of power series. Some talks: [RPA] [TAMADI][SeaMac][RAIM2017]

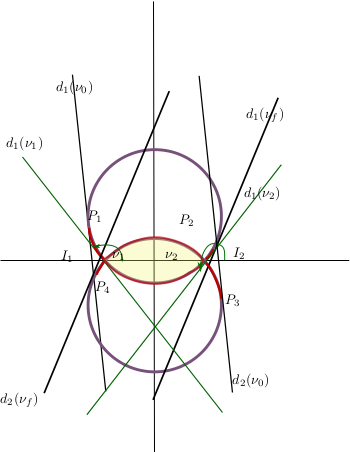
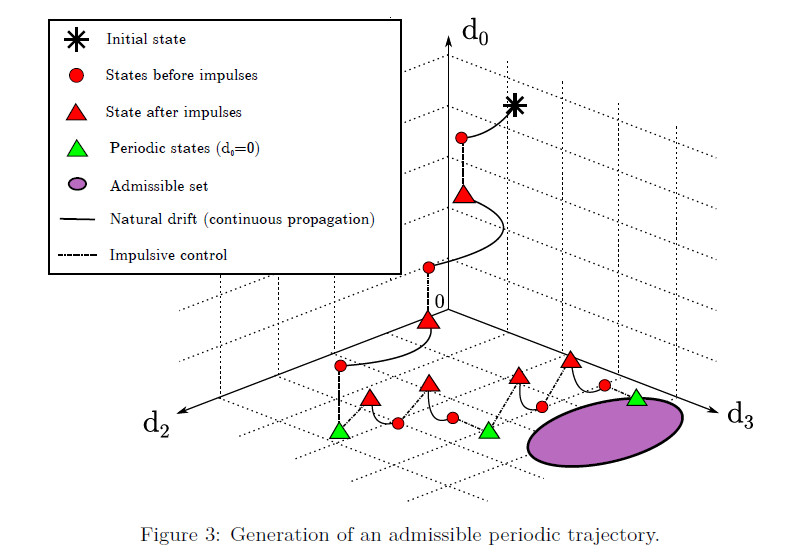
C. Applications to Optimal Control and Aerospace:

  • We proposed a new accurate, reliable and efficient method to compute a certified orbital collision probability between two spherical space objects involved in a short-term encounter under Gaussian-distributed uncertainty. In this model of conjunction, the probability of collision is reduced to the integral of a 2D Gaussian probability density function over a disk. Our computational method is based on an analytic expression for the integral, derived by use of Laplace transform and D-finite functions [C14, C15, J6]. This work is to be extended to long term or multiple encounters during the R&T CNES project Global Collision Probability and Satellites Station Keeping (started 09/16). Talks: [JNCF] [CAPA] [CMS16]

With Denis Arzelier, Florent Bréhard, and Jean-Bernard Lasserre, we are currently attempting to approximately reconstruct the support of the initial collision-prone states in a two-objects long-term encounter. A preliminary result at ISSAC2019 has received the Distinguished Paper Award [C4]. Given a finite number of numerically computed moments for a measure with holonomic density, and assuming a real algebraic boundary for the support, we develop a method for obtaining the coefficients of a polynomial vanishing on this boundary.

  • A new numerical convergent algorithm based on semi-infinite convex optimization for linearized impulsive fixed-time fuel-optimal space rendezvous. Its solution is then used in a general simple procedure dedicated to the computation of the optimal velocity increments and optimal impulses locations. It is also shown that the semi-infinite convex programming has an analytical solution obtained via a simple geometrical construction for the out-of-plane rendezvous problem.[C5, C10] Talks: [Fastrelax16]
  • With Paulo Arantes Gilz, Christophe Louembet et Frédéric Camps, we proposed a model predictive control strategy for the hovering phases of the impulsive spacecraft rendezvous. The path constraints (box-type and periodicity) are satisfied continuously in time, based on a particular parametrization of the linearized relative spacecraft trajectories. Hardware-in-the-loop simulations, using a synthesized LEON3 microprocessor which is compatible with space devices, are performed to assess the efficiency and robustness of the proposed approach[J2] [C6][C9]. Paulo defended his PhD Thesis, co-supervised with Christophe Louembet, on 17 October 2018.

Recent Software:

Students:

Exhaustive List of Publications

Books

[B1]   J.-M. Muller, N. Brunie, F. de Dinechin, C.-P. Jeannerod, M. Joldes, V. Lefèvre, G. Melquiond, N. Revol, and S. Torres, Handbook of Floating-Point Arithmetic. Birkhäuser, 2018.

International peer-reviewed journals

[J1]   N. Brisebarre, M. Joldeş, J.-M. Muller, A.-M. Naneş, and J. Picot, “Error analysis of some operations involved in the Cooley-Tukey Fast Fourier Transform,” ACM Trans. Math. Softw., vol. 46, May 2020. https://hal.archives-_ouvertes.fr/hal-_01949458/file/Bounds-_FFT-_HAL.pdf.

[J2]   P. R. Arantes Gilz, M. Joldes, C. Louembet, and F. Camps, “Stable Model Predictive Strategy for Rendezvous Hovering Phases Allowing for Control Saturation,” Journal of Guidance, Control, and Dynamics, vol. 42, no. 8, pp. 1658–1675, 2019. https://hal.archives-_ouvertes.fr/hal-_01678768.

[J3]   F. Bréhard, N. Brisebarre, and M. Joldeş, “Validated and numerically efficient Chebyshev spectral methods for linear ordinary differential equations,” ACM Transactions on Mathematical Software (TOMS), vol. 44, no. 4, p. 44, 2018. https://hal.archives-_ouvertes.fr/hal-_01526272/.

[J4]   M. Joldes, J.-M. Muller, and V. Popescu, “Tight and rigorous error bounds for basic building blocks of double-word arithmetic,” ACM Transactions on Mathematical Software (TOMS), vol. 44, no. 2, p. 15, 2017. https://hal.archives-_ouvertes.fr/hal-_01351529v3.

[J5]    A. Benoit, M. Joldes, and M. Mezzarobba, “Rigorous uniform approximation of D-finite functions using Chebyshev expansions,” Mathematics of Computation, vol. 86, no. 305, pp. 1303–1341, 2016. https://hal.archives-_ouvertes.fr/hal-_01022420.

[J6]   R. Serra, D. Arzelier, M. Joldes, J.-B. Lasserre, A. Rondepierre, and B. Salvy, “Fast and accurate computation of orbital collision probability for short-term encounters,” Journal of Guidance, Control, and Dynamics, vol. 39, no. 5, pp. 1009–1021, 2016. https://hal.archives-_ouvertes.fr/hal-_01132149/.

[J7]   M. Joldes, O. Marty, J.-M. Muller, and V. Popescu, “Arithmetic algorithms for extended precision using floating-point expansions,” IEEE Transactions on Computers, vol. 65, pp. 1197–1210, April 2016. https://hal.archives-_ouvertes.fr/hal-_01111551v2.

[J8]   M. Joldes, V. Popescu, and W. Tucker, “Searching for sinks for the Hénon map using a multiple-precision GPU arithmetic library,” SIGARCH Comput. Archit. News, vol. 42, no. 4, pp. 63–68, 2014. https://hal.archives-_ouvertes.fr/hal-_00957438.

[J9]   S. Chevillard, J. Harrison, M. Joldes, and C. Lauter, “Efficient and accurate computation of upper bounds of approximation errors,” Theoretical Computer Science, vol. 16, no. 412, pp. 1523–1543, 2011.

Publications in the peer-reviewed proceedings of international conferences

[C1]   M. Joldeş and B. Paşca, “Efficient Floating-Point Implementation of the Probit Function on FPGAs,” in Application-specific Systems, Architectures and Processors (ASAP), 2020 IEEE 31st International Conference on, pp. 173–180, 2020. Best Paper Award, https://hal.archives-_ouvertes.fr/hal-_02875528/.

[C2]   M. Joldeş and J.-M. Muller, “Algorithms for manipulating quaternions in floating-point arithmetic,” in Computer Arithmetic (ARITH), 2020 IEEE 27th Symposium on, pp. –to appear–, 2020. https://hal.archives-_ouvertes.fr/hal-_02470766/.

[C3]   D. Arzelier, F. Bréhard, and M. Joldes, “Exchange algorithm for evaluation and approximation error-optimized polynomials,” in Computer Arithmetic (ARITH), 2019 IEEE 26th Symposium on, pp. 30–37, 2019. https://hal.archives-_ouvertes.fr/hal-_02006606/.

[C4]   F. Bréhard, M. Joldes, and J.-B. Lasserre, “On moment problems with holonomic functions,” in Proceedings of the 2019 on International Symposium on Symbolic and Algebraic Computation, ISSAC ’19, (New York, NY, USA), pp. 66–73, ACM, 2019. Distinguished Paper Award, https://hal.archives-_ouvertes.fr/hal-_02006645.

[C5]   R. Serra, D. Arzelier, F. Bréhard, and M. Joldes, “Fuel-optimal impulsive fixed-time trajectories in the linearized circular restricted 3-body-problem,” in IAF Astrodynamics Symposium in 69TH international astronautical congress, pp. 1–9, 2018. https://hal.archives-_ouvertes.fr/hal-_01830253.

[C6]   F. Camps, P. R. A. Gilz, M. Joldes, and C. Louembet, “Embedding a SDP-based control algorithm for the orbital rendezvous hovering phases,” in Proceedings of tof IEEE International Conference on Integrated Navigation Systems, Jun 2018, Saint Petersburg, Russia. 10.23919/ICINS.2018.8405931, pp. 1–7, IEEE, 2018. https://hal.laas.fr/hal-_01729956.

[C7]   M. Joldes, J.-M. Muller, and V. Popescu, “Implementation and performance evaluation of an extended precision floating-point arithmetic library for high-accuracy semidefinite programming,” in Computer Arithmetic (ARITH), 2017 IEEE 24th Symposium on, pp. 27–34, IEEE, 2017. https://hal.archives-_ouvertes.fr/hal-_01491255/.

[C8]   S. Boldo, M. Joldes, J.-M. Muller, and V. Popescu, “Formal verification of a floating-point expansion renormalization algorithm,” in International Conference on Interactive Theorem Proving, pp. 98–113, Springer, 2017. https://hal.archives-_ouvertes.fr/hal-_01512417/document.

[C9]    P. R. A. Gilz, M. Joldes, C. Louembet, and F. Camps, “Model predictive control for rendezvous hovering phases based on a novel description of constrained trajectories,” in IFAC-PapersOnLine, vol. 50, pp. 7229–7234, Elsevier, 2017. https://hal.laas.fr/hal-_01484764.

[C10]   D. Arzelier, F. Bréhard, N. Deak, M. Joldes, C. Louembet, A. Rondepierre, and R. Serra, “Linearized impulsive fixed-time fuel-optimal space rendezvous: A new numerical approach,” in Proceedings of the 20th IFAC Symposium on Automatic Control in Aerospace, 21-25 August, 2016, Sherbrooke, Quebec, Canada, vol. 49, pp. 373–378, 2016. https://hal.archives-_ouvertes.fr/hal-_01275427.

[C11]   S. Collange, M. Joldes, J.-M. Muller, and V. Popescu, “Parallel floating-point expansions for extended-precision GPU computations,” in Proceedings of ASAP 2016: The 27th Annual IEEE International Conference on Application-specific Systems, Architectures and Processors, 6-8 July 2016, London, England, pp. 139–146, IEEE, 2016. https://hal.archives-_ouvertes.fr/hal-_01298206.

[C12]   F. Bréhard, N. Brisebarre, and M. Joldes, “A new efficient algorithm for computing validated Chebyshev approximations solutions of linear differential equations,” in SCAN 2016: 17th International Symposium on Scientific Computing,Computer Arithmetic and Verified Numerics, Uppsala, Sweden, Sept. 2016, pp. 41–43, 2016.

[C13]   M. Joldes, J.-M. Muller, V. Popescu, and W. Tucker, “Campary: Cuda multiple precision arithmetic library and applications,” in Mathematical Software – ICMS 2016: 5th International Conference, Berlin, Germany, July 11-14, 2016, Proceedings (G.-M. Greuel, T. Koch, P. Paule, and A. Sommese, eds.), (Cham), pp. 232–240, Springer International Publishing, 2016. https://hal.archives-_ouvertes.fr/hal-_01312858.

[C14]   R. Serra, D. Arzelier, M. Joldes, J.-B. Lasserre, A. Rondepierre, and B. Salvy, “A new method to compute the probability of collision for short-term space encounters,” in Astrodynamics Specialist Conference, pp. 1–7, Aug 2014.

[C15]   R. Serra, D. Arzelier, M. Joldes, and A. Rondepierre, “Probabilistic collision avoidance for long-term space encounters via risk selection,” in Advances in Aerospace Guidance, Navigation and Control, pp. 679–698, Springer, Dec 2015. https://hal.archives-_ouvertes.fr/hal-_01995936/document.

[C16]   M. Joldes, J. Muller, and V. Popescu, “On the computation of the reciprocal of floating point expansions using an adapted Newton-Raphson iteration,” in IEEE 25th International Conference on Application-Specific Systems, Architectures and Processors, ASAP 2014, Zurich, Switzerland, June 18-20, 2014, pp. 63–67, IEEE, 2014. https://hal.archives-_ouvertes.fr/docs/00/95/73/79/PDF/invNewton.pdf.

[C17]   N. Brisebarre, M. Joldes, É. Martin-Dorel, M. Mayero, J. Muller, I. Pasca, L. Rideau, and L. Théry, “Rigorous polynomial approximation using Taylor Models in Coq,” in NASA Formal Methods - 4th International Symposium, NFM 2012, Norfolk, VA, USA, April 3-5, 2012. Proceedings (A. Goodloe and S. Person, eds.), vol. 7226 of Lecture Notes in Computer Science, pp. 85–99, Springer, 2012.

[C18]   N. Brisebarre, M. Joldes, P. Kornerup, É. Martin-Dorel, and J. Muller, “Augmented precision square roots and 2-d norms, and discussion on correctly rounding sqrt(x^2+y^2),” in 20th IEEE Symposium on Computer Arithmetic, ARITH 2011, Tübingen, Germany, 25-27 July 2011 (E. Antelo, D. Hough, and P. Ienne, eds.), pp. 23–30, IEEE Computer Society, 2011.

[C19]   N. Brisebarre and M. Joldes, “Chebyshev interpolation polynomial-based tools for rigorous computing,” in Symbolic and Algebraic Computation, International Symposium, ISSAC 2010, Munich, Germany, July 25-28, 2010, Proceedings (W. Koepf, ed.), pp. 147–154, ACM, 2010.

[C20]   F. de Dinechin, M. Joldes, and B. Pasca, “Automatic generation of polynomial-based hardware architectures for function evaluation,” in 21st IEEE International Conference on Application-specific Systems Architectures and Processors, ASAP 2010, Rennes, France, 7-9 July 2010 (F. Charot, F. Hannig, J. Teich, and C. Wolinski, eds.), pp. 216–222, IEEE, 2010.

[C21]   F. de Dinechin, M. Joldes, B. Pasca, and G. Revy, “Multiplicative square root algorithms for FPGAs,” in International Conference on Field Programmable Logic and Applications, FPL 2010, August 31 2010 - September 2, 2010, Milano, Italy, pp. 574–577, IEEE, 2010.

[C22]   S. Chevillard, M. Joldes, and C. Q. Lauter, “Sollya: An environment for the development of numerical codes,” in Mathematical Software - ICMS 2010, Third International Congress on Mathematical Software, Kobe, Japan, September 13-17, 2010. Proceedings (K. Fukuda, J. van der Hoeven, M. Joswig, and N. Takayama, eds.), vol. 6327 of Lecture Notes in Computer Science, pp. 28–31, Springer, 2010.

[C23]   S. Chevillard, M. Joldes, and C. Q. Lauter, “Certified and fast computation of supremum norms of approximation errors,” in 19th IEEE Symposium on Computer Arithmetic, ARITH 2009, Portland, Oregon, USA, 9-10 June 2009 (J. D. Bruguera, M. Cornea, D. D. Sarma, and J. Harrison, eds.), pp. 169–176, IEEE Computer Society, 2009.

Publications in the peer-reviewed proceedings of national conferences

[NC1]   M. Joldes, V. Popescu, and W. Tucker, “Searching for sinks of Hénon map using a multiple-precision GPU arithmetic library,” in Forum des Jeunes Mathématicien-ne-s, p. 6, Nov 2013.

[NC2]   M. Joldes, “When a logarithm is a misspelled algorithm,” in Proceedings of the Association Femmes et mathématiques, Sept. 2010.

[NC3]   F. de Dinechin, M. Joldes, B. Pasca, and G. Revy, “Racines carrées multiplicatives sur FPGA,” in SYMPosium en Architectures nouvelles de machines (SYMPA), (Toulouse), Sept. 2009.

Articles under submission, research reports

[R1]   M. Joldes, Validated symbolic-numeric algorithms and practical applications in aerospace. Habilitation à Diriger des Recherches, Université Toulouse III Paul Sabatier. http://homepages.laas.fr/mmjoldes/HDR/HDR.pdf.

[R2]   D. Arzelier, F. Bréhard, M. Joldes, J.-B. Lasserre, M. Léo, and A. Rondepierre, “Global probability of collision: Problem modeling via occupation measures,” Tech. Rep. Version 2.0, LAAS-CNRS, June 2018. CNES Research and Transfer Contract, https://hal.laas.fr/hal-_02077552.

[R3]   M. Joldes, Rigorous Polynomial Approximations and Applications. Thèse, École Normale Supérieure de Lyon - ENS LYON, Sept. 2011. https://tel.archives-_ouvertes.fr/tel-_00657843.