TP2: modeling with P/T nets

For the rest of the course we will be using the tool Tina to edit and analyze Petri nets, see http://projects.laas.fr/tina/.

---

Exercise 1. Modelling

Remember the message-passing example?

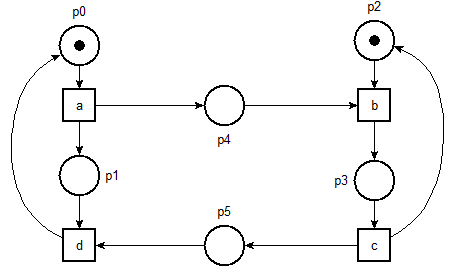
1. Create the model in Tina using the NetDraw editor (nd)

2. Add the possibility to lose a message when going left-to-right (place p4)

3. Add the possibility to re-emit the message if it was lost

---

Exercise 2. Pre- and Post-conditions

Write the (Pre,Post) conditions for the following P/T net

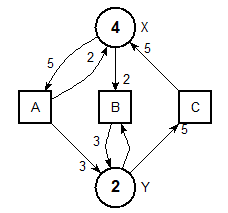
$$A= \left ( \begin{bmatrix} \dots \\\ \dots \end{bmatrix} , \begin{bmatrix} \dots \\\ \dots \end{bmatrix} \right ) \qquad B= \left ( \begin{bmatrix} 2 \\\ 1 \end{bmatrix} , \begin{bmatrix} 0 \\\ 3 \end{bmatrix} \right ) \qquad C= \left ( \begin{bmatrix} \dots \\\ \dots \end{bmatrix} , \begin{bmatrix} \dots \\\ \dots \end{bmatrix} \right )$$

$$m_0= \begin{bmatrix} 4 \\\ 2 \end{bmatrix} = X.4, Y.2$$

Always on the same example:

1. Compute the marking graph.

2. Define the trace language for this net.

3. Draw the net with the editor.

4. Build the marking graph (Tools > reachability), first in verbose mode then in aut format, and check whether you were correct.

5. Find a (good!) reason why this net will always be bounded ($\forall 𝑚_0$).

6. In general, this property depends on the value of $𝑚_0$. Find an example of P/T net that has a finite marking graph on some inputs and not one others.

---

Exercise 3. The printer queue

John wants to print a file. He needs to grab access to the (shared) printer, TP, then to the printer queue, TQ, before releasing, R, the two resources.

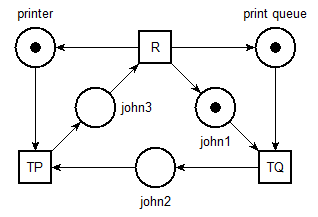
1. Draw the net with the editor.

2. Simulate the behavior (Tools > stepper).

3. Model a second user, Fred, that takes the same resources, but in the other order.

4. “Merge” the two nets.

5. Simulate the behavior (Tools > stepper).

6. Build the marking graph (Tools > reachability), first in verbose mode then in aut format.

---

Exercise 4. The swimming pool

Model the operations in a swimming pool

• A swimming pool has $c$ cabins, where people can undress, and $p$ baskets to deposit clothes.

• A user can enter a cabin (TC) only if a cabin is free.

• Once he has a cabin, he has to wait to take a basket (TB) to change and deposit his clothes.

• Then it releases the cabin and enter the swimming pool (ES).

• He can leave the basin (LS) only if a cabin is free.

• After changing, he leaves his basket (LB) and frees a cabin.

• Finally, he exits (EXIT) the pool.